δοκιμή

Κινηματική

Γωνιακή επιτάχυνση ράβδου και επιτάχυνση σώματος δεμένο με νήμα με αυτήν.

i) Το βασικό ερώτημα είναι το νήμα είναι τεντωμένο ή όχι;

Ας υποθέσουμε ότι το νήμα είναι τεντωμένο οπότε στο σώμα Σ ασκείται η τάση Τ και στη ράβδο η Τ₁ και επειδή το νήμα είναι τεντωμένο Τ=Τ₁. Εξάλλου αφού το νήμα είναι τεντωμένο η ταχύτητα του σημείου Δ είναι ίση με την ταχύτητα κάθε σημείου του νήματος λαρα και του σώματος Σ. Δηλαδή:

υ_Δ=υ_Σ ή

ω(ΑΔ) = υ_Σ και με παραγώγιση:

α_Σ=α_γων·(αΔ) (1)

Εφαρμόζοντας τον θεμελιώδη νόμο της Μηχανικής για το σώμα Σ και για την δοκό έχουμε:

ΣF=m₁·α ή W₁-Τ=m₁·α ή Τ=m₁(g-α) (2)

Στ=Ι·α_γων ή Τ₁(ΑΔ) + W·(ΑΟ) = Ι·α_γων (3)

Με βάση την (2) παίρνουμε από τη σχέση (3):

m₁(g-α) (ΑΔ) +mg(ΑΟ) = 1/3 ml²·α_γων και με βάση την (1)

m₁[g- α_γων·(ΑΔ)]·(ΑΔ) + mg·(ΑΟ) = 1/3 ml²·α_γων (4)

από όπου βρίσκουμε α_γων= 3rad/s².

ii) Οπότε η επιτάχυνση το σώματος Σ είναι:

α_Σ=α_γων·(ΑΔ) =3·2m/s²= 6m/s².

Οπότε Τ=45(10-6) =180Ν

iii) Αν (ΑΔ) =5m με αντικατάσταση στην (4) βρίσκουμε:

α_γων ≈ 2,2 m/s².

Ναι αλλά τότε

Τ=45(10-11)= -45Ν, πράγμα που δεν μπορεί να συμβεί, κατά συνέπεια η τάση του νήματος είναι μηδέν, οπότε το σώμα Σ πέφτει ελεύθερα με επιτάχυνση g=10m/s².

Οπότε εφαρμόζοντας τον θεμελιώδη νόμο της Μηχανικής για την δοκό έχουμε:

Στ=Ι·α_γων ή W·(ΑΟ) = Ι·α_γων

mgl/2 =1/3 ml²·α_γων ή

α_γων= 3g/2l = 30/12 rad/s² =5/3 rad/s².

Τεστ στις Τριβές.

Στο σχήμα έχουν σχεδιαστεί οι δυνάμεις (και οι τριβές).

Κατά την κάθοδο ισχύει:

ΣF_x=m·α ή

Β_x-Τ= m·α₁ (1)

Στην άνοδο:

ΣF_x=m·α ή

Β_x+Τ = m·α₂ (2)

Από τις σχέσεις (1) και (2) προκύπτει ότι η επιτάχυνση είναι μεγαλύτερη κατά μέτρο στην άνοδο.

Μπορείτε να δείτε όλα τα θέματα του Τεστ από ΕΔΩ.

Κυκλικό αγωγός σε μαγνητικό πεδίο.

Α) Ο αγωγός θα δεχθεί δύναμη Laplace, με φορά όπως στο σχήμα, άρα σωστή απάντηση είναι η i).

Β) Με βάση το συμπέρασμα που καταλήξαμε στην Άσκηση Δύναμη Laplace καταλήγουμε ότι

F_L=Β·Ι·2R.

Γ) Σωστή απάντηση με βλαση τα παραπάνω είναι η iii).

Πλαίσιο παράλληλο στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου.

i) Στις πλευρές ΑΒ και ΓΔ δεν ασκούνται δυνάμεις από το πεδίο αφού έχουν την διεύθυνση των δυναμικών γραμμών, ενώ στις πλευρές ΔΑ και ΒΓ δυνάμεις με φορά, όπως στο σχήμα και μέτρα:

F₁=F₂=ΒΙα=2·2·1Ν

ii) Οι δυνάμεις F₁ και F₂ είναι αντίθετες οπότε:

ΣF=F₁-F₂ = 0

iii) Μπορεί η συνισταμένη δύναμη να είναι μηδέν, όμως με την επίδραση των δυνάμεων το πλαίσιο θα περιστραφεί αφού ασκείται ροπή στο πλαίσιο.

Τεστ Ισορροπίας στερεού

i) Οι δυνάμεις που ασκούνται στη ράβδο φαίνονται στο διπλανό σχήμα.

Επειδή η ράβδος ισορροπεί:

ΣF=0 και Στ=0

Ν₁+Ν₂=w =150Ν (1)

Εξάλλου παίρνοντας τις ροπές ως προς το σημείο Γ θα έχουμε:

-w·(ΟΓ) + Ν₂·(ΓΔ) =0 ή

Ν₂=150·1/3 Ν=50Ν

Οπότε από την (1) Ν₁=150Ν-50Ν =100Ν.

ii) Θέτοντας σε περιστροφή τον κινητήρα στο σημείο Δ θα ασκηθεί δύναμη στην ράβδο, με φορά όπως στο σχήμα. Για να ισορροπεί η ράβδος θα αναπτυχθεί και στατική τριβή και από το τρίποδο στο σημείο Γ.
Αφού η ράβδος ισορροπεί Τ₂-Τ₁=0 ή

Τ₁=Τ₂=μΝ₂ =0,6·50Ν= 30Ν

iii) Για να μην ολισθήσει η ράβδος στο σημείο Γ θα πρέπει η ασκούμενη τριβή να είναι στατική.

Τ₁≤Τ_ορ

Τ₁ ≤ μ_s·Ν₁ ή

μ_s ≥ Τ₁/Ν₁

μ_s ≥ 0,3

iii) Ασκώντας κατακόρυφη δύναμη F στο άκρο Α μειώνεται η αντίδραση Ν₂. Η μέγιστη τιμή της δύναμης F, είναι αυτή για την οποία μηδενίζεται η Ν₂, οπότε παίρνοντας τις ροπές ως προς το σημείο Γ θα πάρουμε:

F·(ΑΓ) - w·(ΟΓ) = 0 ή

F= 150·1/2Ν=75Ν

Πρόβλημα μετατόπισης χημικής ισορροπίας

α)

mol/l	Η2 +	Ι2	↔ 2ΗΙ
Αρχικά	x	x
Αντ-παρ	-y	-y	2y
Χ.Ι.	x-y	x-y	2y
	y	y	2y

K_c= [ΗΙ]²/[Η₂][Ι₂] ή

4=[ΗΙ]²/[Η₂]²

2=2y/x-y

2x-2y=2y

2x=4y

x=2y

Άρα [Η₂]=[Ι₂]=0,2Μ και [ΗΙ]=0,4Μ

β) Τη στιγμή t₁ αυξήθηκε η συγκέντρωση του ΗΙ χωρίς να αλλάξει η συγκέντρωση του Η₂, κατά συνέπεια προσθέσαμε στο δοχείο ΗΙ.

γ) Για τη μετατόπιση της ισορροπίας έχουμε:

mol/l	Η2 +	Ι2	↔ 2ΗΙ
Αρχικά	0,2	0,2	0,6
Αντ-παρ	ω	ω	-2ω
Χ.Ι.	0,2+ω	0,2+ω	0,6-2ω

Παίρνοντας τη σταθερά χημικής ισορροπίας θα έχουμε:

K_c= [ΗΙ]²/[Η₂][Ι₂]

4=(0,6-2ω)²/(0,2+ω)²

0,6-2ω=2(0,2+ω)

0,6-2ω=0,4+2ω

0,4ω=0,2

ω=0,05

Έτσι οι τελικές συγκεντρώσεις θα είναι:

mol/l	Η2 +	Ι2	↔ 2ΗΙ
Χ.Ι.	0,25	0,25	0,5

Παράγοντες που επηρεάζουν την θέση της Χημικής ισορροπίας.

Η αντίδραση είναι εξώθερμη οπότε αύξηση της θερμοκρασίας ευνοεί την ενδόθερμη έτσι τελικά η ποσότητα του Ν₂ θα είναι μεγαλύτερη, ενώ επειδή αυξάνεται η ταχύτητα της αντίδρασης η ισορροπία θα αποκατασταθεί σε μικρότερο χρόνο.

Σωστό είναι το διάγραμμα (iv).

Μετατόπιση χημικής ισορροπίας

Αφού μειώσαμε στο μισό τον όγκο του δοχείου, διπλασιάστηκε η πίεση. Με την αύξηση της πίεσης η ισορροπία μετατοπίζεται προς την κατεύθυνση που λιγοστεύουν τα mol, δηλαδή προς τα δεξιά κι έτσι η πίεση γίνεται λιγότερη από 40 atm. Να επανέλθει στην αρχική τιμή των 20 atm δεν είναι δυνατό γιατί το σύστημα τείνει να επαναφέρει την αρχική του κατάσταση.
Έτσι οι σωστές απαντήσεις είναι i) 40 atm, ii) 35 atm

Δύναμη Laplace σε πλαίσιο1.

Στο πλαίσιο ασκούνται οι δυνάμεις που φαίνονται στο σχήμα, όπου:

F₁=ΒΙ(ΑΝ) και F₂=ΒΙ(ΑΡ)

Αναλύουμε την F₂ και παίρνουμε:

F_2x=F₂συνθ=ΒΙ(ΑΡ)·(ΑΝ)/(ΑΡ) =ΒΙ(ΑΝ)=2·2·1Ν=4Ν

F_2y=F₂·ημθ=ΒΙ(ΑΡ).(ΡΝ)/(ΑΡ)=ΒΙ(ΡΝ) =4Ν

Αφού ΡΝ=ΑΝ

ΣF_y=F_2y-F₁ =4N-4N=0 και

ΣF_x = F_2x= 4Ν

Σωληνοειδές μέσα σε ΟΜΠ.

Λαμβάνοντας υπόψη όσα αναπτύχθηκαν στην άσκηση Δύναμη Laplace βρίσκουμε ότι η δύναμη Laplace είναι η ίδια με αυτήν που θα ασκήτο σε ευθύγραμμο αγωγό μήκους l.

Άρα F=ΒΙl=2·5·0,4N=4N

Με φορά όπως στο σχήμα.

Δύναμη Laplace σε τυχαίου σχήματος πλαίσιο.

Οι δυνάμεις έχουν σχεδιαστεί στο σχήμα με μέτρα:

F₁=ΒΙ(ΑΒ) , F₃=ΒΙ(ΑΓ)

Για την F₂, με βάση το σχόλιο που διατυπώσαμε για το σχήμα β, μπορούμε να βρούμε τις δύο συνιστώσες της. Η F_2x θα έχει μέτρο ίσο με τη δύναμη που θα ασκείτο σε ευθύγραμμο αγωγό με μήκος όσο είναι η προβολή του τόξου ΒΓ στην κατακόρυφη διεύθυνση, ενώ η F_2y ίσο με τη δύναμη που θα ασκείτο σε ευθύγραμμο αγωγό με μήκος όσο είναι η προβολή του τόξου ΒΓ στην οριζόντια διεύθυνση:

F_2x= ΒΙ(ΑΒ) = F₁ και

F_2y=ΒΙ(ΑΓ) = F₃.

Οπότε και πάλι

ΣF=0

Δύναμη Laplace σε πλαίσιο

Στο σχήμα έχουν σχεδιαστεί οι δυνάμεις που ασκούνται σε κάθε πλευρά, με μέτρα:

F₁=ΒΙ(ΑΒ), F₂=ΒΙ(ΒΓ), F₃=ΒΙ(ΓΔ) και F₄=ΒΙ(ΑΔ).

Οι συνιστώσες της F₄ είναι:

F_4x=F₄ημθ =ΒΙ(ΑΔ)· (ΑΕ)/(ΑΔ)= ΒΙ(ΑΕ) και

F_4y=ΒΙ(ΑΔ)·συνθ=ΒΙ(ΑΔ)·(ΔΕ)/(ΑΔ)=ΒΙ(ΔΕ)=ΒΙ(ΒΓ)=F₂.

Οπότε:

ΣF_x= F₃+F_4x-F₁=ΒΙ(ΓΔ+ΑΕ-ΑΒ) = 0 και

ΣF_y=F₂-F_4y= 0 άρα και

ΣF= 0

Δύναμη Laplace σε Τριγωνικό πλαίσιο

Στο δεύτερο σχήμα οι δυνάμεις είναι κάθετες στις πλευρές του πλαισίου, όπως στο σχήμα. Για τα μέτρα τους έχουμε:

F₁=ΒΙ(ΑΓ), F₂= ΒΙ(ΓΔ) και F₃=ΒΙ(ΑΔ)

Αναλύουμε την δύναμη F₃ σε δύο συνιστώσες μια με την διεύθυνση της F₁ και μια με την διεύθυνση της F₂ και έχουμε:

F_3x= F₃ημθ= ΒΙ(ΑΔ) · ημθ= ΒΙ(ΑΔ)· (ΑΓ)/(ΑΔ) = ΒΙ(ΑΓ) = F₁.

F_3y=F₃·συνθ= ΒΙ(ΑΔ)·(ΓΔ)/(ΑΔ) = ΒΙ(ΓΔ) = F₂.

Οπότε ΣF_x=F_3x-F₁=0 και

ΣF_y=F₂-F_3y=0

Άρα ΣF = 0

Σχόλιο:

Βλέπουμε ότι στην πλευρά ΓΔ ασκείται μια δύναμη, που η μια συνιστώσα της είναι ίση με την δύναμη που θα ασκήτο στην προβολή της στη διεύθυνση της ΑΓ και η άλλη στην προβολή της στην διεύθυνση ΓΔ.

Δύναμη Laplace σε Τετράγωνο πλαίσιο

Στο πρώτο σχήμα σε κάθε πλευρά του πλαισίου ασκείται η δύναμη που έχει σχεδιαστεί. Για τα μέτρα των δυνάμεων έχουμε:

F₁=ΒΙ(ΑΔ), F₂=ΒΙ(ΑΒ), F₃=ΒΙ(ΒΓ) και F₄=ΒΙ(ΓΔ).

Εύκολα βλέπουμε ότι F₁=F₃ και F₂=F₄, οπότε:

ΣF=0.

Πρόβλημα Οργανικής Χημείας.

α) Η αντίδραση του αλκενίου είναι:

C_νΗ_2ν + Η₂Ο → C_νΗ_2ν+1ΟΗ

x mοl x mol

Αλλά για το αλκένιο:

x=m/Μ_r ή x=5,6/14ν,

ενώ για την αλκοόλη:

x= 9,2/(14ν+18)

από όπου

9,2/(14ν+18) = 5,6/14ν ή

ν=2

άρα το αλκένιο (Α) είναι το CH₂=CH₂ και η αλκοόλη (Β) η CH₃CH₂ΟΗ.

β) Η ποσότητα του Βr₂ είναι n=CV = 0,5·0,2mol=0,1mol.

Με βάση την αντίδραση:

CH2=CH2 + Br2	→ CH2Br-CH2Br
0,1 mol 0,1 mol

Και η ποσότητα του αιθενίου είναι 0,1mol.

CH2=CH2 +	HCl→	CH3 -CH2Cl (Γ)
0,1mol		0,1mol

CH3 -CH2Cl +	KCN →	CH3-CH2-CN + KCl
0,1mol		0,1mol

CH3CH2CN +	2 H2O→	CH3CH2COOH + NH3
0,1mol		0,1mol

CH3CH2COOH +	CH3CH2OH→	CH3CH2COOCH2CH3 + H2O
0,1mol		0,1mol

Η μάζα του προπανικού αιθυλεστέρα είναι:

M=0,1·Μ_r=0,1· 102g=10,2g

Μια άλλη παρασκευή του εστέρα είναι:

CH₃CH₂CΟΟΝα + CH₃CH₂Cl → CH₃CH₂COOCH₂CH₃ + NaCl

Οργανική Χημεία. Αντιδράσεις υποκατάστασης

Επιτρόχια και κεντρομόλος επιτάχυνση.

Στο σχήμα εμφανίζονται οι δυνάμεις που ασκούνται στο σώμα. Αναλύουμε το βάρος σε δύο συνιστώσες, την Β_x στη διεύθυνση του νήματος και την Β_y σε κάθετη διεύθυνση. Για τα μέτρα των δύο συνιστωσών έχουμε:

Β_x= Β·ημθ=mgσυνθ και Β_y=mg·ημθ

α) Η κεντρομόλος επιτάχυνση είναι ίση:

α_κ= υ²/R = 4m/s².

β) ΣF_R=mα_κ ή Τ-Β_x =mα_κ ή Τ= mgσυνθ + mα_κ

Τ=(2·10·1/2+2·4)Ν=18Ν.

γ) Στην διεύθυνση την κάθετη προς το νήμα έχουμε:

ΣF_y=mα_y ή

.

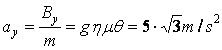Η επιτάχυνση αυτή έχει την διεύθυνση της εφαπτομένης στην κυκλική τροχιά, έχει δηλαδή την διεύθυνση της γραμμικής ταχύτητας και αλλάζει το μέτρο της (σε αντίθεση η κεντρομόλος επιτάχυνση αλλάζει την διεύθυνση της ταχύτητας). Έτσι ο ρυθμός μεταβολής του μέτρου της ταχύτητας είναι:

.

Συνάντηση κινητών στην κυκλική κίνηση.

Η γωνιακή ταχύτητα του Α κινητού είναι:

ω₁= θ/t =(π/3)/2= π/6 rad/s.

Ενώ του κινητού Β:

ω₁= θ/t =(-π/2)/2 = -π/4 rad/s.

Οι γραμμικές ταχύτητες έχουν μέτρα:

υ₁=ω₁/R = π/6R και υ₂= ω₂/R = π/4R

Με διαίρεση κατά μέλη παίρνουμε:

υ₁/υ₂ = (π/6R)/(π/4R) = 2/3 ή 3υ₁=2υ₂.

Έτσι οι απαντήσεις είναι:

Σ

Σ

Σ

Λ

Σχέσεις μεταξύ γραμμικών και γωνιακών μεγεθών στην ΟΚΚ.

α) Για την γραμμική ταχύτητα ισχύει:

υ=2πR/Τ από όπου Τ=2πR/υ = 2π·40/4 s= 20π s=62,8 s.

β) Η γραμμική ταχύτητα είναι ίση:

υ=s/t ή s=υt=4·20 m= 80m

και η γωνία θ=s/R=2 rad.

Η γωνία σε μοίρες είναι:

θ= (θ/2π)·360°=360/π ≈115°.

Ροπή αδράνειας και γωνιακή επιτάχυνση

α) Βρίσκουμε την ροπή αδράνειας του συστήματος ως προς τον άξονα περιστροφής Ο.

Ι=Ι₁+Ι₂

I=[(1/12)ml² +ml²/4]+[(1/12)ml²+md²]

Όπου d=(ΟΚ). Αλλά (ΟΚ)²=(4²+3²)m² ή d=5m.

Ι=100kgm².

Από τον θεμελιώδη νόμο της μηχανικής παίρνουμε:

Στ=Ια_γων ή w·l/2+w·l=Iα_γων

α_γων= 1,8rad/s

β) Η επιτάχυνση του σημείου Κ είναι κάθετη στην ΟΚ και έχει μέτρο:

α_Κ=α_γων·R=α_γων·(ΟΚ) =1,8·5m/s²=9m/s².

Κύλιση ή ολίσθηση του κυλίνδρου;

i) δ
ii) Λ	Σ	Σ	Λ
iii) Λ	Σ	Λ	Λ

Πότε έχουμε καλύτερη ισορροπία;

Έστω ότι έχουμε κρατήσει κατακόρυφα την ράβδο με το χέρι μας και σε απόσταση y υπάρχει η σημειακή μάζα. Αν εκτραπεί κατά μια μικρή γωνία θ και εφαρμόσουμε τον θεμελιώδη νόμο της μηχανικής θα πάρουμε:

Στ=Ι·α_γων ή

mgyημθ= my²·α_γων άρα

α_γων=(gημθ)/y

Παρατηρούμε ότι η γωνιακή επιτάχυνση είναι αντιστρόφως ανάλογη προς το ύψος της μάζας. Συνεπώς μικρότερη επιτάχυνση, άρα και μεγαλύτερη σταθερότητα θα έχουμε όταν η μάζα απέχει 0,6m από το κάτω άκρο της ράβδου.

Υπολογισμός δύναμης από τον άξονα περιστροφής μιας ράβδου.

α) Εφαρμόζοντας τον θεμελιώδη νόμο της Μηχανικής για την στροφική κίνηση παίρνουμε:

Στ=Ι·α_γων

mgημθ·l = 1/3 ml²·α_γων

α_γων=(3gημθ)/l=40rad/s².

β) Εφαρμόζοντας τον θεμελιώδη νόμο της Μηχανικής για την κίνηση του κέντρου μάζας της δοκού έχουμε:

ΣF_x= mυ²/R (1) και

ΣF_y= mα_cm (2)

Από την (1) έχουμε:

F₂-mgσυνθ =mω²R ή

F₂= mgσυνθ + mω²·l/2 *

F₂=(10·10·0,6+10·100·0,3)Ν=360Ν

Ενώ από την (2):

W_y-F₁ = mα_cm ή

F₁=mgημθ-mα_γων·l/2 ή

F₁=(10·10·0,8-10·40·0,3)Ν=200Ν

* από την γνωστή σχέση ημ²θ+συν²θ =1 βρίσκουμε ημθ=0,6.

Για καλύτερη μελέτη της δυναμικής του στερεού που στρέφεται γύρω από σταθερό άξονα, πατήστε ΕΔΩ.

Δυναμική στερεού με σταθερό άξονα περιστροφής.

α) Αφού η ράβδος δεν δέχεται δύναμη από τον άξονα, η μόνη δύναμη που δέχεται είναι το βάρος της. Αλλά ΣF=mα_cm οπότε:

Mg=mα_cm

α_cm=g=10m/s².

β) Αναλύουμε το βάρος σε μια συνιστώσα παράλληλη στη ράβδο και μια κάθετη σε αυτήν.

W_R=W_x = mυ²/R

mgσυνθ =mω²R

ω²=10·0,8/0,5 ή

ω= 4rad/s.

γ)

Και W_y=mα_cm ή

mgημθ = mα_γων·R ή

α_γων=gημθ/R ή *

α_γων=10·0,6/0,5 rad/s² =12 rad/s².

* από την γνωστή σχέση ημ²θ+συν²θ =1 βρίσκουμε ημθ=0,6.

Για καλύτερη μελέτη της δυναμικής του στερεού, πατήστε ΕΔΩ.

Κεντρομόλος δύναμη.

Οι δυνάμεις που ασκούνται στο σώμα είναι το βάρος και η τάση του νήματος, όπως στο σχήμα.

Β=mg=40N

Επειδή το σώμα εκτελεί κυκλική κίνηση:

ΣF=F_κεντρ= mυ²/R ή

Τ-Β= mυ²/R ή

Τ=mg+ mυ²/R=40+4·25/2 =90Ν

Επιταχυνόμενη κυκλική κίνηση.

Σ

Σ

Σ

Σ

Σ

Σ

Ομαλή κυκλική κίνηση 1

Σωστό είναι το γ)

Ομαλή κυκλική κίνηση

α) 2

β) 4

γ) 5

Άσκηση Οριζόντιας βολής.

α) Το σώμα Β εκτελεί ελεύθερη πτώση και έχει κατέβει κατά:

y₂ = ½ gt² = ½ 10·4=20m

Το Α σώμα εκτελεί οριζόντια βολή για την οποία:

x= υ₀·t= 60m/s και y= ½ gt² = ½ 10·4=20m

β) Η μετατόπιση στον κατακόρυφο άξονα και για τα δύο σώματα είναι:

y= ½ gt² ή t² =2y/g = 16s² ή t=4s.

γ) Στην οριζόντια διεύθυνση το Α σώμα εκτελεί ευθύγραμμη ομαλή κίνηση:

x= υ₀t = 120m.

Ενώ υ_y=gt=40m/s και από το πυθαγόρειο θεώρημα παίρνουμε:

υ² = υ_x²+ υ_y² ή υ²=(900+1600)m/s ή υ=50m/s

Και με διεύθυνση που σχηματίζει με την οριζόντια διεύθυνση γωνία θ με

εφθ=υ_y/υ_x=4/3

Οριζόντια βολή.

Το σώμα έχει σταθερή κατακόρυφη επιτάχυνση, ενώ η ταχύτητα μεταβάλλει την διεύθυνσή της.

υ_y= gt = 10m/s και για την τελική ταχύτητα ισχύει:

υ² = υ_x² + υ_y² άρα υ> υ_x.

Οπότε οι απαντήσεις είναι:

Λ

Σ

Λ

Σ

Σ

Σ

Σ

Εκτόξευση τροχού σε οριζόντιο επίπεδο, χωρίς γωνιακή ταχύτητα.

Ο τροχός δέχεται δύναμη τριβής ολίσθησης Τ=μΝ=μmg. Άρα:

Τ=mα ή α=μg

Στ=Ια_γων ή μmgR= ½ mR² α_γων

α_γων= 2μg/R

Η τριβή μηδενίζεται τη στιγμή που η ταχύτητα του σημείου επαφής του τροχού με το έδαφος μηδενιστεί. Όταν δηλαδή:

υ_cm=υ_γρ ή υ= ωR.

Αλλά υ=υ₀- αt και ω=α_γωνt

Οπότε υ₀-αt =α_γωνt·R ή

υ₀= μgt+2μgt ή

t= υ₀/3μg και

υ=υ₀-αt = υ₀-μg·υ₀/3μg=2υ₀/3

Με βάση αυτά η απάντηση είναι:

α) Σ

β) Σ

γ) Σ

δ) Λ

Κύλιση και ολίσθηση τροχού σε λείο επίπεδο.

Για την μεταφορική κίνηση:

ΣF_x= m·α_cm άρα α=F/m

Για την περιστροφική κίνηση:

Στ=Ι·α_γων ή F·R = ½ mR²·α_γων ή α_γων = 2F/mR

Οπότε: α_cm = ½ α_γων·R.

Η επιτάχυνση του σημείου Α είναι ίση με την οριζόντια επιτάχυνση του σημείου Β. Οπότε:

α_Β= α_cm+ α_επ = F/m + (2F/mR)·R= 3 F/m = 3α_cm.

dL/dt=τ=F·R = σταθερή.

Οι απαντήσεις λοιπόν είναι:

Σ

Λ

Σ

Σ

Κύλιση και ολίσθηση τροχού.

Σωστή είναι η πρόταση γ).

Τροχαλία και σώματα.

Για την τροχαλία ισχύει:

Τ₂΄·R-Τ₁΄·R= Ι·α_γων

Οπότε αν έχει μάζα Τ₂΄>Τ₁΄, διαφορετικά Τ₂΄= Τ₁΄.

Οι μάζες συνδέονται με νήμα σταθερού μήκους, κάθε σημείο του οποίου έχει κάθε στιγμή την ίδια ταχύτητα και την ίδια επιτάχυνση. Άρα:

α₂ = α_επ= α₁ = α_γων·R, ενώ

w₂- Τ₂΄= m₂·α₂.

Οπότε οι απαντήσεις είναι:

α) Σ

β) Σ

i) Σ

ii) Σ

iii) Σ

iv) Σ

Διατήρηση Ορμής - Στροφορμής.

Μόλις έρθουν σε επαφή ο τροχός με τη σανίδα, θα ασκηθεί πάνω του τριβή ολίσθησης με φορά προς τα δεξιά, η οποία θα επιταχύνει τον τροχό, ενώ η αντίδρασή της θα ασκηθεί στη σανίδα, με φορά προς τα αριστερά, η οποία θα επιταχύνει τη σανίδα. Το σύστημα είναι μονωμένο και στο σύστημα δεν ασκούνται εξωτερικές ροπές ως προς τον άξονα του τροχού. Η τριβή ολίσθησης μετατρέπει ένα μέρος της Μηχανικής ενέργειας σε θερμότητα. Μόλις το κατώτερο σημείο του τροχού έχει ταχύτητα ίση με την ταχύτητα της σανίδας, η τριβή μηδενίζεται και δεν υπάρχουν πλέον μεταβολές στις ταχύτητες των δύο σωμάτων.

Έτσι οι απαντήσεις είναι:

α) Σ

β) Σ

γ) Σ

δ) Σ

ε) Λ

στ) Λ

Μπορείτε να δείτε την εξέλιξη σε Interactive Physics ( αν το έχετε..) ΕΔΩ.

Οργανική Χημεία. Αντιδράσεις Προσθήκης.1

Οργανική Χημεία. Αντιδράσεις Προσθήκης.2

Οργανική Χημεία. Αντιδράσεις Προσθήκης.

Κίνηση φορτισμένου σωματιδίου σε Μαγνητικό πεδίο.

α) Με την βοήθεια του κανόνα των τριών δακτύλων βρίσκουμε ότι η ένταση του πεδίου είναι όπως στο σχήμα.

β) Η δύναμη Lorenz που δέχεται το σωματίδιο είναι κάθετη στην ταχύτητα στα σημεία εισόδου-εξόδου και παίζει το ρόλο της κεντρομόλου, κατευθύνεται δηλαδή προς το κέντρο του κύκλου. Έτσι το κέντρο της κυκλικής τροχιάς είναι το σημείο Κ όπου (ΕΚ)=(ΜΚ)-(ΜΕ)

Η γωνία ΕΑΚ είναι ίση με θ αφού έχουν τις πλευρές κάθετες και είναι οξείες γωνίες

Άρα (ΕΚ) = 1/2 (ΑΚ)

Από το πυθαγόρειο θεώρημα στο τρίγωνο ΑΕΚ παίρνουμε:

(ΑΚ)² = (ΑΕ)²+ (ΕΚ)² ή

R²=α²+ (R/2)² ή

R² = 16 +R²/4 ή

R= (8·3^1/2) /3 cm.

γ) Για την ακτίνα ισχύει R=mυ/Βq από όπου:

Β=mυ/Rq = 10^-7·2·10⁵/(8·3^1/2) /3·10^-2 = 3^1/2/4 T

δ) Η γωνία ΕΑΚ είναι ίση με θ αφού έχουν τις πλευρές κάθετες και είναι οξείες γωνίες. Άρα η επίκεντρη γωνία που διαγράφει το σωματίδιο είναι η ΑΚΜ= φ= 60° και ο απαιτούμενος χρόνος θα είναι:

t= (60/360)·Τ = Τ/6 =πm/3Βq=4π/3^3/2·10^-7s

Συνολική ροπή και ανατροπή.

Η μέγιστη τιμή της στατικής τριβής, η οριακή τριβή έχει μέτρο:

Τ_ορ=μ_s·Ν = μ_s·mg =0,2·100·10=200Ν

Στον άξονα x η δύναμη F είναι μεγαλύτερη από την μέγιστη τιμή της στατικής τριβής, οπότε ο κύβος επιταχύνεται προς τα δεξιά έχοντας επιτάχυνση:

α_cm=ΣF_x/m =(F-Τ)/m=1m/s².

Το αν ανατρέπεται ή όχι ο κύβος εξαρτάται από το σημείο εφαρμογής της κάθετης αντίδρασης Ν του επιπέδου. Έστω x η απόσταση του φορέα της Ν από το Ο. Παίρνοντας τις ροπές ως προς το κέντρο μάζας Ο και θεωρώντας ότι ο κύβος δεν στρέφεται (δεν ανατρέπεται) παίρνουμε:

Στ=0, -Τ·α/2 + Ν·x= 0, από όπου

x=Τα/2Ν= 0,2m

Βλέπουμε λοιπόν ότι ο φορέας της Ν περνά από τη βάση στήριξης, συνεπώς δεν ανατρέπεται ο κύβος.

Οπότε οι απαντήσεις είναι:

Λ

Λ

Σ

Σ

Λ

Λ

Σ

Τέλος αν πάρουμε την συνολική ροπή ως προς την κορυφή Γ θα έχουμε:

Στ= Τ·0 - Ν·0,8 - F·1 + w·1= (-1000·0,8 – 300 + 1000)Νm = - 100Ν·m.

ΣΧΟΛΙΟ:

Όταν η συνισταμένη των δυνάμεων είναι διάφορη του μηδενός, δηλαδή το σώμα έχει επιτάχυνση, αν στρέφεται, θα στρέφεται γύρω από άξονα που περνά από το κέντρο μάζας.

Αν λοιπόν θέλουμε το στερεό να μην στρέφεται, μόνο ως προς αυτόν τον άξονα η συνολική ροπή θα πρέπει να είναι μηδέν. Ως προς τα υπόλοιπα σημεία μπορεί η ροπή να μην είναι μηδέν, χωρίς να σημαίνει ότι το στερεό θα έχει γωνιακή επιτάχυνση.

Υπολογισμός ροπής δύναμης.

Σωστή πρόταση είναι η γ.

ΖΕΥΓΟΣ ΔΥΝΑΜΕΩΝ ΚΑΙ ΘΕΜΕΛΙΩΔΗΣ ΝΟΜΟΣ ΤΗΣ ΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ.

Οι δυνάμεις που ασκούνται στη δοκό φαίνονται στο σχήμα. Επειδή το κέντρο μάζας της ράβδου βρίσκεται πάνω στον άξονα περιστροφής η συνισταμένη των δυνάμεων είναι ίση με μηδέν. Άρα η δύναμη που δέχεται η ράβδος από τον άξονα είναι κατακόρυφη με φορά προς τα πάνω και κατά μέτρο ίση με το βάρος: F=mg=30Ν.

Το σύστημα των δύο δυνάμεων αποτελεί ζεύγος με ροπή τ= - F·d=4Ν·m, οπότε η ράβδος αποκτά σταθερή γωνιακή επιτάχυνση αφού Στ=Ι·α_γων.

Στ= dL/dt = ΔL/Δt = L/t αφού η ροπή παραμένει σταθερή, οπότε:

L=τ·t= 20kgm²/s.

Το έργο του ζεύγους είναι W=τ·θ = 4·10J = 40J, οπότε αυτή θα είναι και η κινητική ενέργεια της ράβδου, ενώ dΚ/dt = τ·ω = τ·α_γων·t, οπότε οι απαντήσεις είναι:

α) Σ

β) Σ

γ) Λ

δ) Σ

ε) Σ

στ) Σ

ζ) Λ